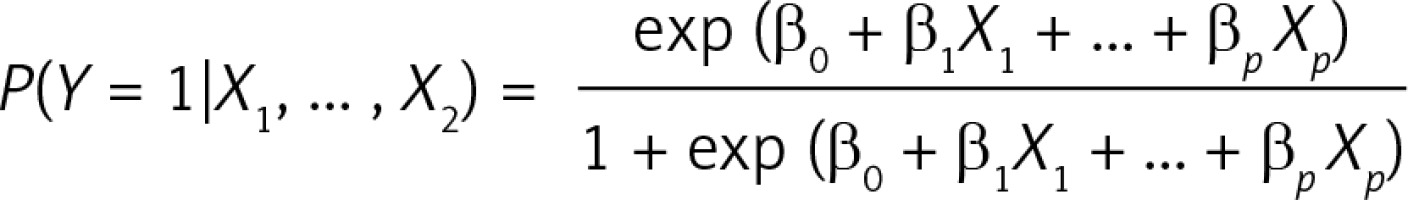Introduction
A lot of medical studies involve the clinical influence of comorbidity factors, which often explain the probability of readmission, mortality [1] or other medical relations [2]. Measures of the overall medical condition of patients seem to be an interesting topic from the point of view of both patients and medical service providers. The literature review on the potential applications of comorbidity measures shows their great impact on many important aspects of healthcare analysis. Charlson et al. [3] introduced a comorbidity index (CCI). The CCI has been developed mainly by Deyo et al. [4], Romano et al. [5] and Elixhauser et al. [6]. Based on Charlson’s concept, with some additional assumptions and improvements in methodology related to 30 groups of comorbid categories and diagnosis-related groups (DRG), Elixhauser et al. used comorbidities to predict in-hospital mortality [6], length of stay at hospitals, and medical expenditure. A systematic review confirmed that Elixhauser’s approach had a good performance in predicting in-hospital death [7]. It was shown [8] that predicting mortality considering the prior 1-year history of patient’s hospitalisations for defining comorbidity yields better results than depending solely on diagnoses from the index hospitalisation.
Risk adjustment is a crucial procedure in treatment quality assessment. We wanted to create a measure that would be based on administrative data only and would enable us to compare the burdens of patients hospitalised for different reasons.
It is clear that the Charlson/Elixhauser approach to comorbidity does not provide such a possibility – cardiac and allergological patients with the same comorbidities would be assigned the same death probability despite the fact that they are obviously different. Moreover, it was shown [6] that for varying primary diagnoses, comorbidities have different effects. For that reason, we introduced Homogeneous Groups – separate models for groups of primary diagnoses. That way, in our risk-adjustment method, we took the primary diagnosis into account in the estimation of both baseline risk and effect of each comorbidity by estimating them separately for each group.
There are more complex risk-adjustment methods with results better than comorbidity-only models. Escobar et al. in [9] achieved a C-statistic of 0.88 by taking into account the laboratory results and admission type. Such an approach has the disadvantage of being inapplicable to administrative databases that do not include such information.
This study aimed to measure the patient’s burden based on administrative data only, using Elixhauser’s approach and to validate the estimation power of models built on homogeneous groups with respect to the main reason for hospitalization.
Material and methods
Homogeneous groups
Our models were created for the heterogeneous group of all admissions and for 21 Homogeneous Groups (HGs). Each HG was defined by a chapter of the International Classification of Diseases, revision 10 (ICD10) published by WHO. Each admission was classified as belonging to a certain HG if the main reason for hospitalisation was included in a corresponding chapter of ICD10.
Approach
Elixhauser’s methodology is based on modelling different explanatory variables such as mortality or length of stay using comorbid variables (CVs) referring to 1-year of medical history. Deyo et al. [4] selected 30 comorbid variables defined by ICD-9-CM codes. Our methodology followed Elixhauser’s approach with only slight changes in definitions of input and output variables. As our models were based on administrative data, we needed to map the ICD10 codes (used in Polish healthcare) onto CVs. Our grouping followed those [10].
Diagnosis-related groups and comorbid variables
To avoid taking into account the main reason for hospitalisation, Elixhauser introduced Diagnosis Related Groups (DRGs) as broader groups of diseases used to screen comorbid variables (CVs). Every CV had its own DRG. For a given CV, its DRG was defined as all morbid conditions for which the diseases might be directly related to the main reason for hospitalisation and not only a coexistent one. In our approach, DRGs were defined as all ICD10 codes that referred to CV and Homogeneous Groups (HG) closely related to that particular CV. HGs related to CVs as well as definitions of CVs are included in Appendix B. It is worth noting that the presence of DRGs is one of the most prominent differences between [6], [3] or [11] approaches.
For every hospitalisation, we determined a value for each of 31 Comorbid Variables as follows:
If the main reason for hospitalisation fell into the DRG of that CV, it was always set to 0.
If a patient suffered from a more severe type of comorbidity, the less severe CV was set to 0; i.e. patients with a DBC (Diabetes, complicated) CV will never have a DBU (Diabetes, uncomplicated) CV. This screening was performed to avoid collinearity of variables.
In other cases, if any ICD10 code which defined a particular CV occurred in secondary diagnoses during the index hospitalisation or any diagnosis up to one year before hospitalisation, then the respective CV was set to 1.
Other input variables in the models were demographic: patient’s age (continuous variable), sex (male/female), and place of residence (town/village).
The outcome variable in our models was the occurrence of a patient’s death during hospitalisation or up to 365 days after discharge, from now on referred to as 1-year mortality. It is important to mention that the gathered data contained complete information about deaths in Poland. Consequently, the outcome variables were free from missing values.
Logistic regression
In our models, we employed logistic regression. The logistic regression model links conditional probability with explaining variables through:
The β0, β1, …, βp coefficients are estimated by the maximum likelihood from the training dataset. Having obtained the above mentioned coefficients, one can estimate the probability of Y = 1 using the values of explanatory variables X 1, …, X p of a record from another (e.g. testing) dataset. In our models, the sum of coefficients β0 + β1 X 1 + ... + βpXp is called the Comorbidity Index, or Comorbidity Score, and it is related to the probability of a patient’s death through the mentioned relation. Since all of our models had the same outcome variable, it made sense to compare results of patients coming from different Homogeneous Groups through a single-number scale of the Comorbidity Index. The odds ratio (OR) for some binary variables X i in this model is simply an exponent of its corresponding coefficient βi. Confidence intervals (CI) for the OR are obtained by exponentiation of βi CI.
At the beginning of the analysis, correlations between comorbidity variables were studied using Pearson correlation. Bidirectional stepwise selection was performed to determine the optimal set of variables. In this procedure, several models with different sets of variables were computed and one minimizing Bayesian information criterion (BIC) was selected. Due to this method, our models had different numbers of CVs and none of them included all. To compare the performance of our models, we produced area under the curve (AUC) statistics (also called C-statistics) for each model. Each analysis was performed in R [12] using the pROC package [13] at the adopted significance level 0.05.
Heterogeneous group model
In order to validate the importance of comorbid factors in predicting 1-year and in-hospital mortality, we first built a logistic regression model containing only demographic variables: patient’s age, sex, and place of residence (baseline model). In the next step, a more complex one, which included Elixhauser’s comorbidity variables, was built. In this case, variable selection was employed.
Homogeneous group models
Subsequently, we wanted to verify the hypothesis that splitting our study population into Homogeneous Groups would allow us to separate the effects of variables for each group of diseases. Sub-models were created separately for each Homogeneous Group. At first, we produced models involving only demographic variables and one of the CVs to obtain unadjusted coefficients. These models served a robustness check for the main model including several comorbidity variables.
Study population
All patients who were registered as hospitalised for any reason in the public health system in 2015 and 2014 were considered in the study. Those data were obtained from the national database of hospitalisations, maintained by the National Health Fund (NFZ). The set included 11 156 668 inpatient stay records from 2015, used as the training population, and 10 888 599 from 2014 used as the testing population. As stated before, in order to determine the values of CVs, 1-year history of treatment prior to each hospitalisation was considered. The history consists both of hospital stays and consultations in outpatient clinics which provided healthcare to the patients. Table I presents the partition of the admissions into Homogeneous Groups (Appendix A). The most numerous groups, both in 2014 and 2015, were Injury, poisoning, and certain other consequences of external causes (about 14%) and Diseases of the circulatory system (about 13%). Additionally, the number of admissions of each group was over 24 thousand and as a result, that gave the opportunity to create a separate model based on HG. Thanks to our access to data from a long period, we decided to test and train our models on the basis of all hospitalisations from two separate years, which allowed us to validate the models in a better manner. We trained the model on the dataset from 2015 to have the estimated coefficients based on the most recent data. The absolute and relative numbers of admissions are similar and relatively big in particular groups.
Table I
Characteristics of study population – homogeneous groups
| Group | Number of admissions in 2015 | Number of admissions in 2014 | ||
|---|---|---|---|---|
| Absolute | Relative (%) | Absolute | Relative (%) | |
| Heterogeneous Group | 11 156 668 | 100 | 10 888 599 | 100 |
| Chapter I – Certain infectious and parasitic diseases | 245 725 | 2.20 | 237 989 | 2.19 |
| Chapter II – Neoplasms | 863 019 | 7.74 | 843 577 | 7.75 |
| Chapter III – Diseases of the blood and blood-forming organs and certain disorders involving the immune mechanism | 97 452 | 0.87 | 96 758 | 0.89 |
| Chapter IV – Endocrine, nutritional and metabolic diseases | 284 565 | 2.55 | 275 873 | 2.53 |
| Chapter V – Mental and behavioural disorders | 330 453 | 2.96 | 328 415 | 3.02 |
| Chapter VI – Diseases of the nervous system | 346 625 | 3.11 | 335 699 | 3.08 |
| Chapter VII – Diseases of the eye and adnexa | 420 138 | 3.77 | 392 407 | 3.60 |
| Chapter VIII – Diseases of the ear and mastoid process | 95 965 | 0.86 | 94 285 | 0.87 |
| Chapter IX – Diseases of the circulatory system | 1 393 634 | 12.49 | 1 408 417 | 12.93 |
| Chapter X – Diseases of the respiratory system | 704 231 | 6.31 | 686 955 | 6.31 |
| Chapter XI – Diseases of the digestive system | 764 138 | 6.85 | 760 803 | 6.99 |
| Chapter XII – Diseases of the skin and subcutaneous tissue | 173 361 | 1.55 | 170 939 | 1.57 |
| Chapter XIII – Diseases of the musculoskeletal system and connective tissue | 482 299 | 4.32 | 454 902 | 4.18 |
| Chapter XIV - Diseases of the genitourinary system | 778 587 | 6.98 | 781 699 | 7.18 |
| Chapter XV – Pregnancy, childbirth and the puerperium | 666 100 | 5.97 | 672 395 | 6.18 |
| Chapter XVI – Certain conditions originating in the perinatal period | 183 421 | 1.64 | 180 138 | 1.65 |
| Chapter XVII – Congenital malformations, deformations and chromosomal abnormalities | 78 973 | 0.71 | 77 219 | 0.71 |
| Chapter XVIII – Symptoms, signs and abnormal clinical and laboratory findings, not elsewhere classified | 664 150 | 5.95 | 628 576 | 5.77 |
| Chapter XIX – Injury, poisoning and certain other consequences of external causes | 1 608 679 | 14.42 | 1 521 496 | 13.97 |
| Chapter XX – External causes of morbidity and mortality | 24 558 | 0.22 | 25 544 | 0.23 |
| Chapter XXI – Factors influencing health status and contact with health services | 950 595 | 8.52 | 914 513 | 8.40 |
| Chapter XXII – Codes for special purposes | 0* | 0 | 0 | 0 |
General characteristics of the study population are presented in Table II (Appendix B). The training and testing sets were similar with respect to presence of considered variables. Mean age was 46.85 in 2015 and 46.56 in 2014. Comorbid variables with the most occurrences were HPT (932 298 cases in 2015 and 890 541 in 2014), CANCER (811 443 in 2015, 777 929 in 2014) and COPD (651 338 in 2015 and 636 396 in 2014). The least present variable was HIV (2 926 cases in 2015 and 2 637 in 2014); it had almost 9 times fewer occurrences than the second the least present variable, BLA (26 098 in 2015 and 27 305 in 2014).
Table II
Characteristics of study population – comorbidities*
* All abbreviations and definitions of variables used in Table I are given in Appendix B.
It is important to understand what is considered to be a record. A single record in this study is a hospitalisation, so each patient can have more than one. Furthermore, we analysed a 1-year post-hospitalisation mortality, so one patient can have several records prior to death. Out of 6 924 639 patients served in 2015, 399 946 died in hospital or up to 1 year after the last hospitalisation, but due to the aforementioned methodology, we considered 11 156 668 records with 1 056 240 cases of 1-year mortality. This approach implies that our models could be applied to assess the patient’s probability of death upon admission for hospitalisation.
Results
The data sets were characterized by a low correlation coefficient – the highest Pearson correlation value was 0.25. Therefore, the considered variables were at low risk of multicollinearity.
Heterogeneous group model
Comparing the baseline model to the one with CVs, the hypothesis that inserting comorbidities improved the performance of the baseline model was confirmed by the ANOVA likelihood-ratio test (p < 0.01). The model with CVs yielded adjusted coefficients presented in Table III. One more time, the ANOVA likelihood-ratio test was applied as well. The presented results showed that all CVs and demographic variables were found significant (p < 0.05). We also found that META (2.52, p < 0.01) and WL (1.89, p < 0.01) were associated the most with the analysed outcome (excluding intercept). Moreover, there were 9 variables which reduce the probability of death: Residence (–0.064, p < 0.01), CA (–0.13, p < 0.01), DEP (–0.24, p < 0.01), HPT (–0.45, p < 0.01), HTC (–0.42, p < 0.01), HTU (–0.17, p < 0.01), OBES (–0.39, p < 0.01), RHEU (–0.13, p < 0.01), VD (–0.08, p < 0.01). The AUC for the heterogeneous group model was 0.81.
Homogeneous group models
Sub-models were created separately for each Homogeneous Group. According to Table IV, which presents the number of included CVs in the models, the model built on the Chapter XIX data (Injury, poisoning and certain other consequences of external causes) excluded only two variables – CA and FD. Twenty-eight variables were included in the models based on data: Chapter II (Diseases of the blood and blood-forming organs and certain disorders involving the immune mechanism), Chapter XIV (Diseases of the genitourinary system), Chapter XVIII (Symptoms, signs and abnormal clinical and laboratory findings, not elsewhere classified). The fewest number of predictors, only 4, were given to the model in the case of Chapter XVI (Certain conditions originating in the perinatal period). As per Table III, predictors which are associated with the explanatory variably are most META – coefficients were in range of 2.5–3.8 (p < 0.01), except in the models based on Chapter II, Chapter XV, Chapter XVI, where this variable appeared to be insignificant or dropped during stepwise selection; CANCER (0.56–2.8) (p < 0.01), except in Chapter II, Chapter XVI; WL (0.59, 2.4), excluding Chapter IV, Chapter XV, Chapter XVI, Chapter XX. Variable VD was used in the case of 4 models; in other performances, VD resulted in being dropped during selection or insignificant (p > 0.05). Variables DEP, HPT, HTC, HTU, and OBES were found to reduce the probability of a patient’s death in every group in which they were significant. There also appeared a few comorbidities which increase death probability in some groups and reduce it in others. These variables are BLA, CA, COPD, DBU, PSYCH, PUD, RHEU, and VD.
Table III A
Effects of comorbidities on 1-year mortality of patients in the heterogeneous group and homogeneous groups – part 11
| Parameter | Heterogeneous Group | Chapter I | Chapter II | Chapter III | Chapter IV | Chapter V | Chapter VI | Chapter VII | Chapter VIII | Chapter IX | Chapter X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | Coefficient | –6.4** | –6.9** | –4.0** | –5.3** | –7.0** | –7.2** | –7.0** | –8.6** | –9.1** | –7.1** | –6.2** |
| 95% CI | (–6.4; –6.4) | (–7.0; –6.8) | (–4.0; –3.9) | (–5.4; –5.2) | (–7.1; –6.9) | (–7.2; –7.1) | (–7.1; –6.9) | (–8.8; –8.4) | (–9.5; –8.8) | (–7.1; –7.0) | (–6.3; –6.2) | |
| Age | Coefficient | 0.059** | 0.072** | 0.039** | 0.053** | 0.07** | 0.069** | 0.059** | 0.06** | 0.066** | 0.070** | 0.064** |
| 95% CI | (0.059; 0.059) | (0.071; 0.073) | (0.038; 0.039) | (0.052; 0.054) | (0.069; 0.071) | (0.068; 0.070) | (0.058; 0.060) | (0.058; 0.062) | (0.060; 0.071) | (0.070; 0.071) | (0.063; 0.064) | |
| Sex (male) | Coefficient | 0.393** | 0.36** | 0.45** | 0.38** | 0.44** | 0.58** | 0.48** | 0.51** | 0.65** | 0.27** | 0.26** |
| 95% CI | (0.389; 0.398) | (0.32; 0.40) | (0.44; 0.46) | (0.34; 0.42) | (0.41; 0.47) | (0.54; 0.62) | (0.45; 0.52) | (0.46; 0.55) | (0.47; 0.83) | (0.26; 0.28) | (0.24; 0.27) | |
| Residence (village) | Coefficient | –0.064** | –0.088** | –0.044** | –0.13** | –0.042* | 0.045 | – | –0.087** | – | –0.035** | – |
| 95% CI | (–0.069; –0.059) | (–0.13; –0.049) | (–0.056; –0.032) | (–0.17; –0.087) | (–0.073; –0.01) | (0.01; 0.08) | (–0.13; –0.04) | (–0.046; –0.024) | ||||
| HIV | Coefficient | 0.8** | 0.43** | 0.78** | 2.9** | – | – | 2.2** | – | – | 0.82* | 1.4** |
| 95% CI | (0.67; 0.92) | (0.19; 0.67) | (0.40; 1.1) | (2.2; 3.7) | (1.4; 3.0) | (0.27; 1.3) | (0.87; 1.9) | |||||
| ALCO | Coefficient | 0.78** | 0.91** | 0.44** | 0.8** | 1.3** | – | 1.2** | 1.1** | 1.2** | 1.2** | 0.89** |
| 95% CI | (0.76; 0.79) | (0.81; 1.0) | (0.39; 0.50) | (0.65; 0.94) | (1.2; 1.4) | (1.1; 1.3) | (0.89; 1.3) | (0.62; 1.8) | (1.1; 1.2) | (0.83; 0.94) | ||
| BLA | Coefficient | 0.41** | 0.52** | 0.37** | – | 0.26* | 0.75** | – | 0.91** | – | 0.51** | 0.33** |
| 95% CI | (0.38; 0.45) | (0.25; 0.78) | (0.30; 0.43) | (0.099; 0.41) | (0.38; 1.1) | (0.51; 1.3) | (0.43; 0.58) | (0.17; 0.49) | ||||
| CA | Coefficient | –0.13** | – | –0.14** | –0.10** | –0.098** | 0.13** | – | – | – | – | –0.033 |
| 95% CI | (–0.14; –0.12) | (–0.16; –0.12) | (–0.16; –0.042) | (–0.14; –0.055) | (0.058; 0.2) | (–0.058; –0.008) | ||||||
| CANCER | Coefficient | 1.22** | 0.96** | – | 1.8** | 1.5** | 0.59** | 1.2** | 0.77** | 1.2** | 0.56** | 1.0** |
| 95% CI | (1.21; 1.23) | (0.91; 1.0) | (1.7; 1.8) | (1.5; 1.5) | (0.5; 0.68) | (1.2; 1.3) | (0.71; 0.83) | (0.91; 1.4) | (0.54; 0.58) | (1.0; 1.1) | ||
| CHF | Coefficient | 0.74** | 0.85** | 0.57** | 0.40** | 0.71** | 0.64** | 0.75** | 0.84** | 0.91** | – | 0.69** |
| 95% CI | (0.73; 0.75) | (0.79; 0.9) | (0.55; 0.59) | (0.34; 0.45) | (0.67; 0.74) | (0.57; 0.71) | (0.69; 0.81) | (0.77; 0.9) | (0.58; 1.2) | (0.67; 0.72) | ||
| COAG | Coefficient | 1.15** | 0.70** | 0.99** | – | 0.64** | 0.60** | 0.83** | 0.81** | 1.6** | 0.75** | 0.86** |
| 95% CI | (1.13; 1.17) | (0.61; 0.79) | (0.96; 1.0) | (0.51; 0.76) | (0.43; 0.76) | (0.65; 1.0) | (0.58; 1.0) | (0.91; 2.3) | (0.7; 0.8) | (0.77; 0.94) | ||
| COPD | Coefficient | 0.16** | – | 0.24** | –0.20** | –0.15** | – | –0.074 | 0.27** | – | 0.15** | – |
| 95% CI | (0.15; 0.17) | (0.23; 0.26) | (–0.27; –0.14) | (–0.21; –0.10) | (–0.14; –0.01) | (0.20; 0.33) | (0.13; 0.16) | |||||
| DA | Coefficient | 0.47** | 0.61** | 0.32** | – | 0.28** | 0.5** | 0.57** | – | – | 0.51** | 0.44** |
| 95% CI | (0.45; 0.49) | (0.49; 0.73) | (0.28; 0.36) | (0.19; 0.36) | (0.36; 0.64) | (0.39; 0.75) | (0.46; 0.55) | (0.36; 0.51) | ||||
| DBC | Coefficient | 0.28** | 0.39** | 0.29** | 0.24** | – | 0.4** | 0.36** | 0.51** | 0.75** | 0.25** | 0.24** |
| 95% CI | (0.27; 0.29) | (0.33; 0.45) | (0.26; 0.31) | (0.17; 0.31) | (0.32; 0.48) | (0.29; 0.43) | (0.45; 0.57) | (0.39; 1.1) | (0.23; 0.26) | (0.21; 0.27) | ||
| DBU | Coefficient | 0.22** | – | 0.25** | 0.13* | – | 0.14* | 0.24** | 0.27** | – | 0.045** | 0.087** |
| 95% CI | (0.21; 0.23) | (0.22; 0.28) | (0.042; 0.23) | (0.038; 0.25) | (0.14; 0.33) | (0.14; 0.39) | (0.022; 0.068) | (0.042; 0.13) | ||||
| DEP | Coefficient | –0.24** | –0.36** | –0.098** | –0.15 | –0.24** | – | –0.26** | – | – | –0.43** | –0.20** |
| 95% CI | (–0.26; –0.22) | (–0.49; –0.23) | (–0.13; –0.063) | (–0.28; –0.016) | (–0.34; –0.14) | (–0.37; –0.16) | (–0.47; –0.38) | (–0.26; –0.14) | ||||
| DRUG | Coefficient | 0.11** | – | 0.16 | – | – | – | – | – | – | 0.17* | 0.23* |
| 95% CI | (0.062; 0.151) | (0.023; 0.29) | (0.058; 0.29) | (0.072; 0.39) | ||||||||
| FED | Coefficient | 0.89** | 0.50** | 1.2** | 0.59** | – | 0.45** | 1.0** | 0.58** | 1.1** | 0.78** | 0.80** |
| 95% CI | (0.88; 0.91) | (0.43; 0.58) | (1.1; 1.2) | (0.49; 0.70) | (0.36; 0.54) | (0.90; 1.1) | (0.39; 0.77) | (0.44; 1.7) | (0.75; 0.81) | (0.75; 0.85) | ||
| HPT | Coefficient | –0.45** | –0.54** | –0.42** | –0.18** | – | –0.38** | –0.49** | –0.49** | –0.53 | –0.62** | –0.51** |
| 95% CI | (–0.46; –0.43) | (–0.65; –0.44) | (–0.45; –0.39) | (–0.27; –0.091) | (–0.50; –0.27) | (–0.59; –0.39) | (–0.6; –0.37) | (–1.0; –0.089) | (–0.65; –0.59) | (–0.56; –0.46) | ||
| HTC | Coefficient | –0.42** | –0.53** | –0.21** | –0.3** | –0.69** | –0.41** | –0.5** | –0.29** | –0.98** | – | –0.66** |
| 95% CI | (–0.43; –0.41) | (–0.60; –0.47) | (–0.23; –0.18) | (–0.37; –0.23) | (–0.74; –0.64) | (–0.49; –0.32) | (–0.57; –0.43) | (–0.37; –0.21) | (–1.5; –0.55) | (–0.69; –0.63) | ||
| HTU | Coefficient | –0.17** | –0.44** | –0.026** | –0.21** | –0.54** | –0.12** | –0.24** | –0.18** | –0.25 | – | –0.40** |
| 95% CI | (–0.18; –0.16) | (–0.49; –0.4) | (–0.04; –0.011) | (–0.26; –0.16) | (–0.57; –0.5) | (–0.17; –0.076) | (–0.28; –0.19) | (–0.24; –0.12) | (–0.49; –0.011) | (–0.42; –0.38) | ||
| LD | Coefficient | 0.48** | 0.66** | 0.30** | 0.22** | 0.12* | 0.53** | 0.44** | 0.27* | 0.65 | 0.44** | 0.45** |
| 95% CI | (0.46; 0.49) | (0.56; 0.75) | (0.27; 0.34) | (0.13; 0.32) | (0.04; 0.20) | (0.46; 0.59) | (0.33; 0.56) | (0.093; 0.45) | (0.062; 1.2) | (0.41; 0.48) | (0.38; 0.51) | |
| LYMP | Coefficient | 0.55** | 1.1** | – | 1.1** | 1.2** | 0.93** | 1.2** | 1.3** | 1.1 | 0.96** | 1.1** |
| 95% CI | (0.53; 0.57) | (1.0; 1.3) | (1.0; 1.2) | (1.0; 1.3) | (0.58; 1.3) | (1.0; 1.5) | (1.1; 1.4) | (0.12; 1.9) | (0.90; 1.0) | (1.0; 1.2) | ||
| META | Coefficient | 2.52** | 2.9** | – | 3.0** | 3.8** | 2.6** | 3.7** | 2.6** | 2.7** | 2.8** | 2.9** |
| 95% CI | (2.51; 2.53) | (2.7; 3.1) | (2.9; 3.1) | (3.7; 3.9) | (2.3; 3) | (3.5; 3.8) | (2.4; 2.8) | (1.9; 3.4) | (2.7; 2.9) | (2.8; 2.9) | ||
| NEU | Coefficient | 0.52** | 0.79** | 0.44** | 0.27** | 0.70** | 0.54** | – | 0.41** | 1.0** | 0.52** | 0.98** |
| 95% CI | (0.5099; 0.5342) | (0.71; 0.87) | (0.4; 0.47) | (0.16; 0.38) | (0.63; 0.77) | (0.49; 0.59) | (0.29; 0.53) | (0.6; 1.4) | (0.49; 0.54) | (0.94; 1.0) | ||
| OBES | Coefficient | –0.39** | –0.34** | –0.41** | –0.27* | – | –0.36* | –0.55** | –0.62** | – | –0.45** | –0.19** |
| 95% CI | (–0.41; –0.36) | (–0.52; –0.17) | (–0.46; –0.35) | (–0.46; –0.089) | (–0.58; –0.15) | (–0.73; –0.38) | (–0.91; –0.35) | (–0.49; –0.41) | (–0.27; –0.12) | |||
| PARA | Coefficient | 0.84** | 0.94** | 1.1** | – | 0.54** | 0.37* | – | 0.79** | 1.4* | 0.72** | 1.2** |
| 95% CI | (0.81; 0.87) | (0.74; 1.1) | (1; 1.2) | (0.37; 0.72) | (0.12; 0.6) | (0.44; 1.1) | (0.36; 2.3) | (0.66; 0.77) | (1.1; 1.3) | |||
| PCD | Coefficient | 0.82** | 0.92** | 0.76** | 0.26* | 0.50** | 0.72** | 0.68** | 0.44** | 1.9** | – | 0.75** |
| 95% CI | (0.79; 0.84) | (0.75; 1.1) | (0.71; 0.82) | (0.063; 0.46) | (0.33; 0.67) | (0.49; 0.94) | (0.47; 0.89) | (0.17; 0.7) | (1.0; 2.6) | (0.69; 0.8) | ||
| PSYCH | Coefficient | 0.42** | 0.79** | 0.37** | 0.44** | 0.45** | – | 0.81** | 0.52** | – | 0.75** | 0.73** |
| 95% CI | (0.39; 0.44) | (0.63; 0.95) | (0.3; 0.44) | (0.23; 0.65) | (0.31; 0.58) | (0.65; 0.96) | (0.22; 0.8) | (0.69; 0.81) | (0.65; 0.81) | |||
| PUD | Coefficient | 0.26** | – | 0.4** | – | – | – | – | –0.77* | – | – | – |
| 95% CI | (0.23; 0.29) | (0.34; 0.47) | (–1.4; –0.25) | |||||||||
| PVD | Coefficient | 0.31** | 0.47** | 0.20** | 0.18** | 0.39** | 0.41** | 0.31** | 0.35** | – | – | 0.36** |
| 95% CI | (0.30; 0.32) | (0.41; 0.53) | (0.18; 0.22) | (0.12; 0.25) | (0.35; 0.43) | (0.33; 0.49) | (0.24; 0.37) | (0.28; 0.43) | (0.33; 0.38) | |||
| RF | Coefficient | 0.57** | 0.66** | 0.28** | 0.4** | 0.48** | 0.43** | 0.44** | 0.68** | 0.66* | 0.64** | 0.55** |
| 95% CI | (0.56; 0.58) | (0.6; 0.72) | (0.26; 0.31) | (0.33; 0.46) | (0.43; 0.52) | (0.30; 0.55) | (0.35; 0.54) | (0.59; 0.76) | (0.23; 1.1) | (0.62; 0.66) | (0.51; 0.58) | |
| RHEU | Coefficient | –0.13** | 0.19** | –0.21** | –0.36** | –0.19* | –0.60** | – | 0.22* | – | –0.074** | – |
| 95% CI | (–0.15; –0.11) | (0.083; 0.30) | (–0.26; –0.17) | (–0.48; –0.24) | (–0.31; –0.072) | (–0.86; –0.35) | (0.083; 0.35) | (–0.11; –0.035) | ||||
| VD | Coefficient | –0.08** | – | –0.15** | – | – | 0.15 | – | – | – | – | – |
| 95% CI | (–0.09; –0.06) | (–0.18; –0.11) | (0.016; 0.28) | |||||||||
| WL | Coefficient | 1.89** | 1.7** | 2** | 1.1** | – | 1.2** | 1.9** | 0.59 | 1.8 | 1.8** | 1.7** |
| 95% CI | (1.857; 1.905) | (1.6; 1.9) | (1.9; 2) | (0.98; 1.3) | (0.98; 1.3) | (1.7; 2.1) | (0.089; 1.0) | (0.14; 2.9) | (1.7; 1.8) | (1.7; 1.8) | ||
Table III B
Effects of comorbidities on 1-year mortality of patients in the Heterogeneous Group and Homogeneous Groups – part 21
| Parameter | Chapter XI | Chapter XII | Chapter XIII | Chapter XIV | Chapter XV | Chapter XVI | Chapter XVII | Chapter XVIII | Chapter XIX | Chapter XX | Chapter XXI | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | Coefficient | –6.3** | –8.0** | –9.1** | –8.7** | –11.0** | –8.3** | –5.4** | –6.8** | –8.8** | –7.9** | –4.8** |
| 95% CI | (–6.4; –6.3) | (–8.1; –7.8) | (–9.2; –9) | (–8.8; –8.7) | (–12.0; –9.9) | (–8.6; –8.0) | (–5.5; –5.2) | (–6.8; –6.7) | (–8.9; –8.8) | (–8.4; –7.5) | (–4.8; –4.8) | |
| Age | Coefficient | 0.056** | 0.078** | 0.073** | 0.085** | 0.072** | 0.1** | 0.029** | 0.065** | 0.084** | 0.064** | 0.032** |
| 95% CI | (0.056; 0.057) | (0.076; 0.080) | (0.071; 0.075) | (0.084; 0.086) | (0.047; 0.097) | (0.085; 0.12) | (0.026; 0.032) | (0.060; 0.061) | (0.084; 0.085) | (0.059; 0.070) | (0.032; 0.033) | |
| Sex (male) | Coefficient | 0.24** | 0.14** | 0.49** | 0.26** | – | – | 0.21* | 0.36** | 0.53** | 0.70** | 0.43** |
| 95% CI | (0.22; 0.26) | (0.096; 0.19) | (0.45; 0.54) | (0.24; 0.28) | (0.082; 0.34) | (0.34; 0.38) | (0.51; 0.55) | (0.51; 0.90) | (0.42; 0.44) | |||
| Residence (village) | Coefficient | –0.076** | –0.071* | – | –0.023 | – | – | –0.31** | –0.12** | –0.08** | – | –0.033** |
| 95% CI | (–0.095; –0.056) | (–0.12; –0.022) | (–0.046; –0.001) | (–0.48; –0.15) | (–0.14; –0.098) | (–0.1; –0.058) | (–0.045; –0.021) | |||||
| HIV | Coefficient | 1.1* | 1.3 | 2.0* | 2.1** | – | – | – | 1.6** | 0.74* | – | – |
| 95% CI | (0.38; 1.7) | (0.018; 2.3) | (0.18; 3.3) | (1.1; 2.9) | (1.0; 2.0) | (0.19; 1.2) | ||||||
| ALCO | Coefficient | 1.3** | 1.2** | 0.86** | 1.4** | 2.2** | – | – | 0.79** | 1.3** | 1.2** | 0.36** |
| 95% CI | (1.3; 1.3) | (1.0; 1.3) | (0.68; 1.0) | (1.3; 1.5) | (1.2; 2.9) | (0.72; 0.85) | (1.2; 1.3) | (0.98; 1.5) | (0.30; 0.42) | |||
| BLA | Coefficient | 0.32** | – | – | 1.0** | – | – | – | – | –0.39* | – | –0.15** |
| 95% CI | (0.22; 0.41) | (0.88; 1.1) | (–0.64; –0.15) | (–0.22; –0.074) | ||||||||
| CA | Coefficient | –0.15** | – | 0.13** | – | 1.0* | – | – | –0.24** | – | – | – |
| 95% CI | (–0.18; –0.12) | (0.058; 0.21) | (0.18; 1.7) | (–0.27; –0.20) | ||||||||
| CANCER | Coefficient | 1.1** | 0.80** | 0.97** | 1.1** | 2.8** | – | 0.83** | 1.7** | 0.68** | 0.87** | 1.7** |
| 95% CI | (1.0; 1.1) | (0.72; 0.88) | (0.90; 1.0) | (1.1; 1.2) | (2.0; 3.5) | (0.52; 1.1) | (1.7; 1.7) | (0.64; 0.72) | (0.54; 1.2) | (1.6; 1.7) | ||
| CHF | Coefficient | 0.95** | 0.94** | 0.90** | 1.0** | – | 3.0** | 1.8** | 0.83** | 0.86** | 0.72** | 0.29** |
| 95% CI | (0.93; 0.98) | (0.88; 1.0) | (0.83; 0.98) | (1.0; 1.1) | (2.1; 3.7) | (1.6; 1.9) | (0.80; 0.87) | (0.82; 0.9) | (0.37; 1.1) | (0.26; 0.32) | ||
| COAG | Coefficient | 1.6** | 0.97** | 0.79** | 1.1** | – | – | 0.99** | 0.95** | 0.98** | – | 0.69** |
| 95% CI | (1.6; 1.6) | (0.77; 1.2) | (0.59; 0.99) | (0.98; 1.2) | (0.56; 1.4) | (0.86; 1.0) | (0.87; 1.1) | (0.65; 0.72) | ||||
| COPD | Coefficient | –0.14** | –0.26** | 0.15** | –0.089** | – | – | – | –0.05* | –0.18** | – | 0.41** |
| 95% CI | (–0.18; –0.11) | (–0.35; –0.17) | (0.076; 0.23) | (–0.13; –0.051) | (–0.086; –0.013) | (–0.23; –0.14) | (0.39; 0.43) | |||||
| DA | Coefficient | 0.24** | 0.70** | 0.46** | 0.70** | – | – | – | 0.32** | 0.36** | – | 0.15** |
| 95% CI | (0.18; 0.30) | (0.53; 0.87) | (0.26; 0.66) | (0.63; 0.77) | (0.22; 0.42) | (0.25; 0.47) | (0.099; 0.20) | |||||
| DBC | Coefficient | 0.40** | 0.48** | 0.49** | 0.53** | 1.9** | – | 0.40 | 0.37** | 0.40** | – | 0.21** |
| 95% CI | (0.37; 0.44) | (0.41; 0.55) | (0.40; 0.58) | (0.50; 0.57) | (0.87; 2.8) | (0.011; 0.77) | (0.33; 0.42) | (0.34; 0.45) | (0.18; 0.24) | |||
| DBU | Coefficient | 0.22** | 0.22** | 0.15 | 0.27** | – | – | – | 0.29** | 0.29** | –1.2 | 0.16** |
| 95% CI | (0.18; 0.27) | (0.095; 0.35) | (0.012; 0.29) | (0.21; 0.33) | (0.23; 0.36) | (0.22; 0.37) | (–2.7; –0.23) | (0.13; 0.19) | ||||
| DEP | Coefficient | –0.34** | –0.54** | –0.34** | –0.34** | – | – | – | –0.52** | –0.28** | – | –0.055* |
| 95% CI | (–0.41; –0.28) | (–0.74; –0.35) | (–0.50; –0.18) | (–0.42; –0.25) | (–0.60; –0.45) | (–0.35; –0.20) | (–0.089; –0.021) | |||||
| Parameter | Chapter XI | Chapter XII | Chapter XIII | Chapter XIV | Chapter XV | Chapter XVI | Chapter XVII | Chapter XVIII | Chapter XIX | Chapter XX | Chapter XXI | |
| DRUG | Coefficient | – | – | 0.93** | 0.31 | – | – | – | – | 0.78** | 0.66 | 0.34** |
| 95% CI | (0.56; 1.3) | (0.069; 0.55) | (0.67; 0.89) | (0.072; 1.2) | (0.20; 0.47) | |||||||
| FED | Coefficient | 0.72** | 1.5** | 0.79** | 1.1** | – | 5.4** | 0.66* | 0.67** | 0.7** | – | 0.71** |
| 95% CI | (0.67; 0.77) | (1.4; 1.6) | (0.61; 0.96) | (1.1; 1.1) | (3.3; 6.8) | (0.17; 1.1) | (0.61; 0.73) | (0.62; 0.77) | (0.66; 0.75) | |||
| HPT | Coefficient | –0.56** | –0.82** | –0.62** | –0.57** | – | – | – | –0.62** | –0.69** | – | –0.15** |
| 95% CI | (–0.61; –0.50) | (–0.97; –0.67) | (–0.75; –0.50) | (–0.63; –0.51) | (–0.69; –0.56) | (–0.77; –0.61) | (–0.18; –0.13) | |||||
| HTC | Coefficient | –0.67** | –0.50** | –0.43** | –0.17** | – | – | –0.97** | –0.61** | –0.58** | – | –0.21** |
| 95% CI | (–0.71; –0.64) | (–0.59; –0.40) | (–0.53; –0.35) | (–0.21; –0.14) | (–1.3; –0.69) | (–0.65; –0.57) | (–0.63; –0.53) | (–0.23; –0.18) | ||||
| HTU | Coefficient | –0.39** | –0.39** | – | –0.099** | 1.3* | – | –0.52** | –0.3** | –0.21** | – | –0.11** |
| 95% CI | (–0.42; –0.37) | (–0.45; –0.33) | (–0.13; –0.071) | (0.39; 2.0) | (–0.78; –0.28) | (–0.33; –0.27) | (–0.25; –0.18) | (–0.13; –0.097) | ||||
| LD | Coefficient | – | 0.29** | 0.48** | 0.77** | – | 3.8** | 0.57* | 0.71** | 0.64** | 0.73** | 0.28** |
| 95% CI | (0.13; 0.44) | (0.33; 0.64) | (0.70; 0.83) | (1.5; 5.6) | (0.17; 0.94) | (0.65; 0.77) | (0.56; 0.71) | (0.29; 1.1) | (0.24; 0.32) | |||
| LYMP | Coefficient | 0.82** | 0.81** | 1.1** | 1.6** | 2.2 | – | 1.9** | 1.2** | 0.99** | 1.4 | 0.37** |
| 95% CI | (0.7; 0.93) | (0.57; 1.0) | (0.9; 1.4) | (1.5; 1.7) | (–0.64; 3.8) | (0.99; 2.7) | (1.1; 1.3) | (0.85; 1.1) | (0.18; 2.6) | (0.34; 0.4) | ||
| META | Coefficient | 3.3** | 3.0** | 3.4** | 3.7** | – | – | 3.1** | 3.7** | 2.7** | 2.5** | 2.5** |
| 95% CI | (3.2; 3.3) | (2.8; 3.3) | (3.2; 3.6) | (3.6; 3.8) | (2.4; 3.9) | (3.6; 3.7) | (2.6; 2.8) | (1.6; 3.4) | (2.4; 2.5) | |||
| NEU | Coefficient | 0.43** | 0.79** | 0.44** | 0.57** | – | – | 0.58** | 0.41** | 0.82** | 0.64** | 0.38** |
| 95% CI | (0.38; 0.48) | (0.69; 0.90) | (0.32; 0.57) | (0.51; 0.62) | (0.29; 0.85) | (0.36; 0.46) | (0.77; 0.86) | (0.30; 0.96) | (0.34; 0.42) | |||
| OBES | Coefficient | –0.27** | – | –0.56** | –0.17** | – | – | – | –0.69** | –1.0** | – | –0.31** |
| 95% CI | (–0.36; –0.19) | (–0.81; –0.33) | (–0.27; –0.078) | (–0.83; –0.56) | (–1.2; –0.83) | (–0.38; –0.25) | ||||||
| PARA | Coefficient | 0.67** | 1.2** | 1.2** | 0.89** | 3.4* | 6.9** | 1.5** | 0.84** | 0.7** | – | 0.72** |
| 95% CI | (0.53; 0.80) | (0.99; 1.4) | (0.96; 1.4) | (0.76; 1.0) | (0.47; 4.9) | (3.9; 8.8) | (1.0; 1.9) | (0.70; 0.98) | (0.56; 0.85) | (0.62; 0.82) | ||
| PCD | Coefficient | 0.63** | 0.51** | 1.2** | 0.61** | – | – | 1.4** | 0.64** | 0.58** | – | 0.54** |
| 95% CI | (0.51; 0.73) | (0.23; 0.77) | (0.97; 1.4) | (0.49; 0.73) | (1; 1.7) | (0.53; 0.74) | (0.43; 0.72) | (0.48; 0.6) | ||||
| PSYCH | Coefficient | 0.37** | 0.61** | 0.51* | 0.77** | – | – | 1.1* | –0.19* | 0.39** | – | – |
| 95% CI | (0.26; 0.47) | (0.37; 0.83) | (0.17; 0.82) | (0.66; 0.89) | (0.24; 1.7) | (–0.33; –0.059) | (0.28; 0.49) | |||||
| PUD | Coefficient | – | – | –0.63* | 0.41** | – | – | – | –0.32** | –1.6** | – | 0.2** |
| 95% CI | (–1.1; –0.19) | (0.26; 0.56) | (–0.48; –0.17) | (–1.9; –1.4) | (0.13; 0.27) | |||||||
| PVD | Coefficient | 0.33** | 0.68** | 0.49** | 0.55** | – | – | 0.61** | 0.35** | 0.33** | – | 0.22** |
| 95% CI | (0.29; 0.36) | (0.62; 0.74) | (0.40; 0.57) | (0.52; 0.59) | (0.29; 0.92) | (0.31; 0.39) | (0.28; 0.37) | (0.19; 0.25) | ||||
| RF | Coefficient | 0.69** | 0.63** | 0.83** | – | 3.7** | – | 1** | 0.47** | 0.46** | – | 0.33** |
| 95% CI | (0.65; 0.73) | (0.54; 0.73) | (0.73; 0.92) | (2.8; 4.4) | (0.79; 1.2) | (0.42; 0.52) | (0.40; 0.51) | (0.30; 0.37) | ||||
| RHEU | Coefficient | –0.12* | – | – | 0.16** | – | – | – | –0.48** | –0.29** | – | – |
| 95% CI | (–0.19; –0.047) | (0.084; 0.24) | (–0.58; –0.38) | (–0.39; –0.19) | ||||||||
| VD | Coefficient | – | – | – | – | – | – | 0.26 | – | – | – | – |
| 95% CI | (0.0032; 0.51) | |||||||||||
| WL | Coefficient | 1.6** | 2.4** | 1.3** | 2.1** | – | – | 1.5** | 1.7** | 1.3** | – | 0.94** |
| 95% CI | (1.5; 1.6) | (2.2; 2.6) | (1..0; 1.6) | (2; 2.2) | (0.86; 2.0) | (1.6; 1.8) | (1.2; 1.5) | (0.88; 0.99) | ||||
Table IV
C-statistics and number of significant variables for each model
Approach comparison
Table IV presents the quality of each Homogeneous Group model. There were several models with very good performance (rank 1 to 9) and as many with quite good performance (rank 10 to 18). The low predictive power of the last 3 models requires some explanation, which has been covered in the discussion section. Having compared the AUC of the Heterogeneous Group model to homogeneous ones, 13 models of subgroups yielded a C-statistic value higher than the Heterogeneous Group model (AUC > 0.81). It is important to understand that although some Homogeneous Group models had an AUC below 0.81, they were still better classifiers than the Heterogeneous Group model for particular hospitalisations.
Discussion
Homogeneous group approach
Thanks to the introduction of Homogeneous Groups, we were able to determine the difference in baseline risk between the groups. We see that the effects of comorbidities differ between groups, which supports the thesis that a division of the population is needed to obtain a good classifier.
It is worth noting that using the Homogeneous Group approach did not produce separate results. All records could be put on a single Comorbidity Index scale with one, clear, group-independent interpretation. Moreover, the CI produced a measurement that assumes only information about the demography of the patients and the diseases they suffer from, excluding the number of admissions and disease duration.
Lastly, using this methodology, we have singled out fields of medicine in which comorbidity is not applicable in such a simple approach and those in which it is very accurate.
Administrative data approach
Our models required only the admission data and 1-year prior medical history for each hospitalisation. This methodology made it easy to create and evaluate them on big datasets which integrate records from different hospitals.
Our study population was many times bigger than in any preceding study of comorbidity. We have retrieved records from many hospitals with a variety of specialisations. Thanks to that, our results were more general, because they are not affected by the standards of treatment in any particular hospital or by selection bias.
Low performance homogeneous groups
This section explains the poor estimation power and gives suggestions on enhancing the approach to comorbidity for 3 models with the lowest C-statistics: Chapter XV – Pregnancy, childbirth and the puerperium, Chapter XVI – Certain conditions originating in the perinatal period, and Chapter II – Neoplasms.
Having analysed the results of Chapter XV – Pregnancy, childbirth and the puerperium, it was found that the training set for this group consisted of 666 100 hospitalisations, out of which only 166 were cases of 1-year mortality. Therefore, the number of positive observations was not enough to identify a well-fitted model. Perhaps another outcome variable should be defined in order to employ comorbidity for this group.
In the case of Chapter XVI – Certain conditions originating in the perinatal period, the mortality rate in this group was higher than in the case of Chapter XV, but still low. Moreover, the number of hospitalisations was lower – and there were only 69 cases of 1-year mortality. There is another reason why comorbidity could not meet the requirements of this subject. This group consists almost exclusively of new-born children with no diseases (99%), so there was no distinction between the records. This group cannot be analysed through comorbidity at all.
The Chapter II – Neoplasms group has neither of the aforementioned problems: this group displays both high diversity in terms of comorbidity and high mortality. The treatment of neoplasms is often a complex path with several rehospitalisations. To build a model for predicting deaths of oncological patients, one would need to put much more thought into the analysis of a patient’s medical history by adding variables denoting the number of admissions in respect of a HG that could differentiate the observations Moreover, this group was not very homogeneous (e.g. it consists of both malignant and non-malignant neoplasms) and further division is advised.
Negative effects of some comorbidities
Some comorbidities have been found to have a negative impact on mortality (in at least a few HGs), namely: depression, hypertension, hypothyroidism, obesity, peptic ulcer disease, and blood loss anaemia. The same effects were identified in [6] and attributed to administrative data unreliability, especially in reporting diagnoses of low importance in seriously ill patients.
Comparison to other studies
The results based our models performed as well as or better than other comorbidity-only methods for predicting patient mortality [8, 11–13]. So far, the best performing comorbidity-based risk adjustment models have been reported by Escobar et al. [9]. However, their explanatory variables included laboratory results which are not always easy to obtain, and not all patients have the same pre-admission tests.
A major limitation of this study was the reliance on administrative data, which was not recorded for research as much as it was for reimbursement. Its quality depended on the coding procedures, gaps in clinical information and the expenditure context [14–16], so it might not be complete. Some changes in grouping related to coding procedures specific to Polish healthcare could be applied.
The second limitation was insufficient homogeneity of considered groups. Most of them include both urgent care hospitalisations and long the lasting treatment. In our partition, we did not consider severity of a disease, which widely varies within each group. Further splitting of groups should improve the predictive power of models.
The third limitation is the poor performance of models in a few groups. Our approach did not produce a well-performing comorbidity measure for patients treated for neoplasms, during pregnancy and in the perinatal period.
In conclusion, our results support the thesis that comorbidity properly describes mortality in Homogeneous Groups of patients. In terms of C-statistics, most models performed better than the one based on the whole population. Differences in the importance of particular variables among models were observed. We have created models which were very well suited for risk adjustment – they are the best in the literature among those which can be based solely on administrative data (e.g. not on laboratory results). In addition, all of our models can be condensed into one, uniform, single-number comorbidity scale that summarizes all of the patient’s burden.